|
Учебное пособие |
Цены и ценообразованиеРаздел: Экономика
|
2.3.2. КОЭФФИЦИЕНТ ПРЯМОЙ ЭЛАСТИЧНОСТИ СПРОСА ПО ЦЕНЕ: ПОНЯТИЕ И ИСЧИСЛЕНИЕ
Коэффициент прямой эластичности спроса по цене характеризует отношение относительного изменения объема спроса к относительному изменению цены и показывает, на сколько процентов изменяется объем спроса на товар при изменении его цены на 1%. Следовательно, его можно записать как
![]() (2.1)
(2.1)
Выделяют дуговую и точечную эластичность. Пусть дана какая-либо функция спроса:
Q1= f(P1),
где Q1 – объем спроса на данный товар;
P1– цена данного товара.
Изобразим эту функцию графически (рис. 2.5).

Рис.2.5. Определение дуговой эластичности
Предположим, что указанной функции спроса соответствует кривая, на которой произвольно взяты точки Е1 и E2. Причем точка Е1 характеризуется ценой P1 и объемом спроса Q1, а точка E2 – ценой Р2 и объемом спроса Q2. Очевидно, что при переходе от точки Е1 к точке E2 цена снижается с уровня P1 до уровня P2, а объем спроса возрастает от Q1 до Q2.
При расчете эластичности по вышеприведенной формуле неизбежно возникает следующий вопрос: если значения ΔQ и ΔР могут быть однозначно найдены и графически, и аналитически, поскольку определяются как ΔQ = Q2 – Q1; ΔР = Р2 – Р1, то какие значения Р и Q следует принять в качестве весов: базисные (Р1 и Q1) или новые (Р2 и Q2). Очевидно, что применение различных значений Р и Q приведет к разным результатам. Вследствие этого величины Р и Q для расчета коэффициента эластичности определяются чаще всего по правилу средних точек, то есть используются средние для данного интервала значения цены и спроса, а именно:
![]()
Формула (2.1) принимает в этом случае вид:
![]() (2.2)
(2.2)
Таким образом, дуговая эластичность определяется как средняя эластичность.
Здесь следует иметь в виду, что любая функция спроса, проходящая через данные точки, будет характеризоваться одним и тем же коэффициентом эластичности, хотя форма самой дуги (ее кривизна) может быть различной. Иначе говоря, при расчете учитываются только крайние значения спроса и цены и не принимается во внимание реальный характер функции спроса между ними.
Эта формула используется, когда процентные изменения цены и количества достаточно велики, чтобы привести к существенному продвижению вдоль кривой спроса.
В том случае, когда функция спроса носит непрерывный характер, дуговая эластичность заменяется точечной, понимаемой как предел дуговой эластичности по мере того, как длина дуги стремится к нулю, то есть при бесконечно малом изменении цены.
В этом случае:
![]() (2.3)
(2.3)
Одновременно следует учитывать, что действие закона спроса приводит к тому, что значение коэффициента прямой эластичности – величина отрицательная. Вследствие этого, перед формулой, по которой он рассчитывается, обычно ставится знак минус (-), с тем, чтобы получить положительную величину. Однако такой подход не соответствует общему определению эластичности функции, поэтому обычно знак минус перед числовым значением коэффициента эластичности игнорируется, и он определяется по модулю. В случае, если закон спроса не выполняется (товар Гиффена), коэффициент эластичности спроса по цене положителен.
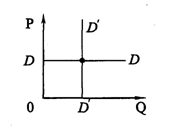
Рис. 2.6. Функция спроса с неограниченной
и нулевой эластичностью
Величина коэффициента эластичности может заметно различаться в зависимости от функции спроса: он может изменяться от 0 до ∞.
На рис. 2.6 линия DD характеризует функцию спроса с эластичностью е = ∞, или, иначе говоря, с неограниченной эластичностью, при которой любое малое изменение цены вызывает значительное изменение спроса, а линия D'D' – функцию спроса с нулевой эластичностью, при которой объем спроса не реагирует на изменение цены.
Для дальнейшего анализа рассмотрим линейную функцию спроса (рис. 2.7).
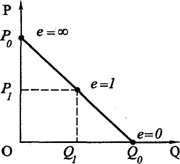
Рис. 2.7. Линейная функция спроса
Эластичность этой функции изменяется в зависимости от уровня цены: если цена стремится к нулю, эластичность также стремится к нулю (в точке Q0), по мере возрастания цены и ее приближения к Р0, эластичность стремится к бесконечности. В середине этого интервала (при Р1 = Р0/2), коэффициент эластичности равен -1.
На этом же рисунке для цен выше цены Р1 соответствующей объему спроса ОQ1, ценовая эластичность больше 1, для цен ниже P1 – спрос неэластичен. Иначе говоря, эластичность спроса выше при высоких и средних ценах и ниже – при низких ценах.
Отсюда следует, что если функция спроса является линейной, а ее график представляет собой прямую линию, то эластичность принимает различные значения в каждой точке графика. Следовательно, без предварительного измерения невозможно сказать, является ли в данной точке спрос эластичным или относительно неэластичным.
Вместе с тем наблюдается значительная связь между значением эластичности и наклоном линии спроса. При более пологой форме линии спроса величина коэффициента эластичности выше, чем в случае более крутой с точки зрения ее наклона линии спроса.
Из вышесказанного можно сделать вывод, что коэффициент эластичности – во всех случаях величина переменная при данной функции спроса. Однако бывают ситуации, когда эластичность спроса на всем протяжении какого-либо отрезка равна 1. В этом случае Р0Q0 = P1Q1. График такой функции является равнобочной гиперболой и асимптотически приближается к осям координат, никогда не пересекаясь с ними.
Рассмотрим, каким образом повлияет эластичность спроса на поведение покупателей. Здесь можно выделить несколько вариантов:
· если спрос совершенно эластичный (е = ∞), то при снижении цены покупатели повышают объем спроса на неограниченную величину, а при повышении цены – полностью отказываются от товара;
· при эластичном спросе (е > 1) при снижении цены объем спроса повышается более высокими темпами по сравнению с изменением цены, а при ее повышении – снижается в более значительных размерах, чем цена;
· при единичной эластичности (е = 1) объем спроса изменяется теми же темпами, что и цена, но в противоположном направлении;
· если спрос неэластичный (е < 1), то при повышении цены объем спроса снижается более низкими темпами, чем растет цена, а при ее снижении – увеличивается более медленно, чем падает цена;
· при совершенно неэластичном спросе (е = 0) любое изменение цены объема спроса совершенно не меняет.
К содержанию книги: Цены и ценообразование
Смотрите также:
Цены и ценообразование Цены и ценообразование "Финансовое право" "Хозяйственное право"
ЦЕНООБРАЗОВАНИЕ НА ПРЕДПРИЯТИИ Цена — это количество денег (или ...
|
Во-первых, это сами цены, их виды, структура,
величина, динамика изменения. Во-вторых, ценообразование как способ
установления новых цен и... |
МАРКЕТИНГ. Установление цен на товары: задачи и политика ...
|
Фирмы подходят к проблемам ценообразования
по-разному. В мелких цены часто устанавливаются высшим руководством. В
крупных... |
ЦЕНООБРАЗОВАНИЕ И РЕАЛИЗАЦИЯ ПРОДУКЦИИ порядок изменения свободных ...
|
ЦЕНООБРАЗОВАНИЕ И РЕАЛИЗАЦИЯ ПРОДУКЦИИ ... Свободные оптовые цены (тарифы) и
свободные отпускные цены (сложившегося ... |
МАРКЕТИНГ. Ценообразование. Методика расчета исходной цены
|
Фирмы решают проблему ценообразования, выбирая
себе методику расчета цен, в которой учитывается как минимум одно из
этих. ... |
МЕЖДУНАРОДНАЯ ЦЕНОВАЯ ПОЛИТИКА Международное стратегическое ...
|
Международное стратегическое ценообразование.
Цены устанавливаются непосредственно головной компанией — это часть.
... |
МАРКЕТИНГ. Ценообразование. Политика цен фирмы. Методика расчета ...
|
Краткое изложение основных положений законов,
касающихся проблем ценообразования, дано во об установлении цен
и ... |
|
В период застоя учеными, занимающимися проблемами цен,
высказывались разумные мысли об улучшении ценообразования в стране.
Но... |