|
Учебные пособия |
|
Курс социально-экономической статистики Раздел: Экономика
|
Расстояние между объектами (кластерами) и мера близости
Наиболее трудным и наименее формализованным в задаче классификации является определение понятия однородности объектов.
В общем случае понятие однородности объектов задается введением либо правила вычисления расстояний ρ(xi, хj) между любой парой исследуемых объектов (x1, x2, ...,xn), либо некоторой функцией r(хi, xj), характеризующей степень близости i-го и j-го объектов.
Если задана функция ρ(xi, хj), то близкие с точки зрения этой метрики объекты считаются однородными, принадлежащими к одному классу. Очевидно, что необходимо при этом сопоставлять ρ(xi, хj) с некоторыми пороговыми значениями, определяемыми в каждом конкретном случае по-своему.
Аналогично
используется и мера близости r(xi, хj), при задании
которой мы должны помнить о необходимости выполнения следующих условий:
симметрии r(xi,
хj) = r(xj, хi);
максимального сходства объекта с самим собой r(xi, хi) = ![]() r(xi,
хj), 1 ≤ i, j ≤ п, и
монотонного убывания r(xi,
хj) по мере увеличения ρ(xi, хj), т.е. из ρ(xk, хl)
≥ ρ(xi,
хj) должно следовать неравенство r(xk, хl) ≤ ρ(xi, хj).
r(xi,
хj), 1 ≤ i, j ≤ п, и
монотонного убывания r(xi,
хj) по мере увеличения ρ(xi, хj), т.е. из ρ(xk, хl)
≥ ρ(xi,
хj) должно следовать неравенство r(xk, хl) ≤ ρ(xi, хj).
Выбор метрики, или меры близости, является узловым моментом исследования, от которого в значительной степени зависит окончательный вариант разбиения объектов на классы при данном алгоритме разбиения. В каждом конкретном случае этот выбор должен производиться по-своему, в зависимости от целей исследования, физической и статистической природы наблюдений, априорных сведений о характере вероятностного распределения X.
Рассмотрим наиболее широко используемые в задачах кластерного анализа расстояния и меры близости.
Обычное евклидово расстояние определяется по формуле
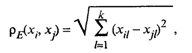 (53.43)
(53.43)
где xil, хjl — значения l-го признака у i-го (j-го) объекта (l = 1, 2, ..., k, i,j = 1, 2, .... п).
Оно используется в следующих случаях:
а) наблюдения берутся из генеральной совокупности, имеющей многомерное нормальное распределение с ковариационной матрицей вида σ2Ek, где Еk — единичная матрица, т.е. исходные признаки взаимно независимы и имеют одну и ту же дисперсию;
б) исходные признаки однородны по физическому смыслу и одинаково важны для классификации.
Естественное с геометрической точки зрения евклидово пространство может оказаться бессмысленным (с точки зрения содержательной интерпретации), если признаки измерены в разных единицах. Чтобы исправить положение, прибегают к нормированию каждого признака путем деления центрированной величины на среднее квадратическое отклонение и переходят от матрицы Х к нормированной матрице с элементами
![]()
где xil — значение l-го признака у i-го объекта;
![]() — среднее значение l-го признака;
— среднее значение l-го признака;
![]() —
среднее квадратическое отклонение l-го признака.
—
среднее квадратическое отклонение l-го признака.
Однако эта операция может привести к нежелательным последствиям. Если кластеры хорошо разделимы по одному признаку и не разделимы по другому, то после нормирования дискриминирующие возможности первого признака будут уменьшены в связи с усилением «шумового» эффекта второго.
«Взвешенное» евклидово расстояние определяется из выражения
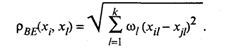 (53.44)
(53.44)
Оно применяется в тех случаях, когда каждой l-й компоненте вектора наблюдений Х удается приписать некоторый «вес» ω1, пропорциональный степени важности признака в задаче классификации. Обычно принимают 0 ≤ ωl ≤ 1, где l = 1,2, ..., k.
Определение весов, как правило, связано с дополнительными исследованиями, например с организацией опроса экспертов и обработкой их мнений. Определение весов ωl только по данным выборки может привести к ложным выводам.
К содержанию книги: Курс социально-экономической статистики
Смотрите также:
СТАТИСТИКА ЭКОНОМИЧЕСКАЯ. Отрасль статистики, изучающая ...
|
СТАТИСТИКА
ЭКОНОМИЧЕСКАЯ. Отрасль статистики, изучающая материальное |
ПРОГНОЗ ЭКОНОМИЧЕСКОЙ АКТИВНОСТИ статистика ...
|
ПРОГНОЗ ЭКОНОМИЧЕСКОЙ
АКТИВНОСТИ ... Вводный курс по |
|
Л.П. Кроливецкой. -
М.: Финансы и статистика, 1996. Березина М.П. |
ОСНОВНЫЕ ВИДЫ ЭКОНОМИЧЕСКОЙ ИНФОРМАЦИИ
|
ОСНОВНЫЕ ВИДЫ ЭКОНОМИЧЕСКОЙ
ИНФОРМАЦИИ ... Статистика дает |
Моделирование рисковых ситуаций в экономике и бизнесе
|
Для студентов,
обучающихся по специальностям «Статистика», « |
Практическое значение экономической теории. Главные ...
|
межотраслевых (экономическая
география, демография, статистика и др.). |
|
Азимов Л.Б.,
Журавская Е.В., Макарова О.Ю. Преподавание экономики в |
Деятельность предприятия. Экономика предприятия
|
М.: Финансы и статистика,
1996. 11. Настольная книга финансиста / Под ред. |
ВНЕШНЕЭКОНОМИЧЕСКИЕ СВЯЗИ Внешнеэкономическая деятельность предприятия