СОВРЕМЕННОЕ ЕСТЕСТВОЗНАНИЕ |
Нестационарная релятивистская космология
|
|
Нестационарная релятивистская космология.
С критикой предложенной Эйнштейном космологической модели выступил наш отечественный выдающийся математик и физик-теоретик А. А. Фридман. Именно А.А. Фридман, опубликовавший свою работу в 1922 г., впервые сделал из общей теории относительности космологические выводы, имеющие поистине революционное значение: он заложил основы нестационарной релятивистской космологии.
Фридман показал, что теоретическая модель Эйнштейна является лишь частным решением гравитационных уравнений для однородных и изотропных моделей, а в общем случае решения зависят от времени. Кроме того, они не могут быть однозначными и не могут дать ответа на вопрос о форме Вселенной, ее конечности или бесконечности. Исходя из противоположного постулата (о возможном изменении радиуса кривизны мирового пространства во времени), Фридман нашел нестационарные решения «мировых уравнений» Эйнштейна.
Встретив решения Фридмана с большим недоверием, Эйнштейн затем убедился в его правоте и согласился с критикой молодого физика. Нестационарные решения уравнений Эйнштейна, основанные на постулатах однородности и изотропии, называются фридмановскими космологическими моделями. Модель Вселенной Фридмана
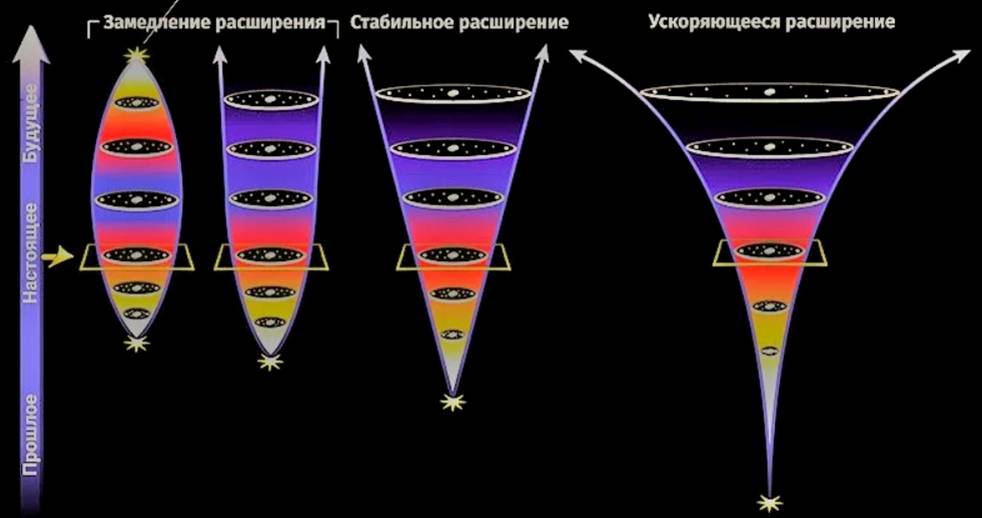
А. А. Фридман показал, что решения уравнений общей теории относительности для Вселенной позволяют построить три возможные модели Вселенной. В двух из них радиус кривизны пространства монотонно растет и Вселенная бесконечно расширяется (в одной модели — из точки; в другой — начиная с некоторого конечного объема). Третья модель рисовала картину пульсирующей Вселенной с периодически изменяющимся радиусом кривизны. Выбор моделей зависит от средней плотности вещества во Вселенной.
Модели расширяющейся Вселенной Фридмана уже вскоре получили удивительно точное подтверждение в непосредственных наблюдениях движений далеких галактик — в эффекте «красного смещения», который свидетельствует о взаимном удалении всех достаточно далеких друг от друга галактик. Таким образом, в настоящее время наблюдается расширение Вселенной. Характер дальнейшей ее эволюции зависит от средней плотности вещества во Вселенной и его отношения с критической плотностью ρ = ЗH2/8πG. Если средняя плотность окажется больше критической, то расширение Вселенной через некоторое время прекратится и сменится сжатием. Если средняя плотность меньше критической, то расширение будет продолжаться неограниченно долго.
В настоящее время критическая плотность определяется величиной 10-29 г/см3. А средняя плотность вещества во Вселенной по современным представлениям оценивается 3 • 10-31 г/см3. Иначе говоря, Вселенная будет сколь угодно долго расширяться. Но определение средней плотности вещества во Вселенной пока ненадежно. Во Вселенной могут присутствовать не обнаруженные еще виды материи, дающие свой вклад в среднюю плотность. И тогда на «вооружение» придется брать «закрытую» модель Вселенной, в которой предполагается, что расширение в будущем сменится сжатием.
Вселенная Фридмана (метрика Фридмана — Леметра — Робертсона — Уокера) — это одна из космологических моделей, удовлетворяющих полевым уравнениям общей теории относительности (ОТО), первая из нестационарных моделей Вселенной.Получена Александром Фридманом в 1922. Модель Фридмана описывает однородную изотропную в общем случае нестационарную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной. Эта работа учёного стала первым основным теоретическим развитием ОТО после работ Эйнштейна 1915—1917 гг.
Термины: работы Фридмана какой закон следовал из моделей фридмана описывающих расширяющуюся вселенную в чем состоит основной вывод Фридмана |
Модель расширяющейся Вселенной
СОДЕРЖАНИЕ: Концепции современного естествознания. Найдыш. Учебник
Последние добавления:
Естествознание Психокоррекционная и развивающая работа с детьми
Введение в культурологию Валеология. Вайнер Валеология
География мирового хозяйства Языковедение
Туристская деятельность Сборник задач по банковскому делу