|
А. А. Корнеев
ЧИСЛОСЛОВНОЕ ДЕРЕВО (Расширенный вариант)
Прежде чем написать более подробно о придуманном мною «Числословном Дереве» и прояснить всё связанное с этим открытием, мне представляется полезным расширить наши представления в сфере нумерологии и эзотерики. Такую интересную возможность предоставляет нам независимый исследователь Виктор Иванович Пьянов.
В своей работе «ОТКРЫТОЕ ПИСЬМО А. ГОРДОНУ» независимый исследователь В.И. Пьянов (полный текст см. на - http://shaping.ru/download/pdffile/pyanov01.pdf ) открывает всем весьма важные моменты, которые, во-первых, требуют своего опубликования в интересах прогресса в расшифровке эзотерических текстов и, во-вторых, для понимания принципов «новой» нумерологии. Ниже, я приведу систематизированные отрывки и цитаты из работы В. И. Пьянова, представляющие значительный интерес для последующего понимания вопросов, связанных с «Числословным Деревом».
В. И. Пьянов пишет о нумерологии следующее: …. Замена букв слова их порядковыми номерами в алфавите современного русского языка выявляет дифференциальную числовую характеристику слова. Создатель учения о логарифмах шотландский математик Джон Непер (1550 - 1617) предложил термин “логарифм”, трактуя перевод этого слова, как специфическое “отношение чисел”. При расшифровке Сценария (имеются ввиду расшифровки египетских источников, связанных с богом Тотом!) оказалось, что обычное деление (определение отношения) двух чисел, являющихся дифференциальными числовыми кальками слов, так же как и логарифмирование числовых калек слов, является эффективным способом познания эзотерического содержания чисел и слов. Вместе с использованием буквенно-числового кода, связывающего слово и число употребимы, в частности, операции логарифмирования, извлечения корня, деления и умножения, которые позволяют получить информацию о сокрытом. В традиционной нумерологии для познания тайной сущности числа допускается: · перестановка цифр в числе · использование аналогов слов · использование анаграмм, · произвольное использование “плавающей” запятой, · многократное умножение (или деление) числа на 2, · выполнение арифметических действий с числами, · сложение цифр числа, · возведение числа в степень (в том числе дробную). В нумерологии путем сложения цифр числа оно сводится к интегральной характеристике и на этой основе нумерологи делают выводы о тайной сущности числа. В. И. Пьяновым предложено (в дополнение к традиционным приемам нумерологии): · логарифмировать числа и ставить между цифрами числа точку (точки), что позволяет читать в числах даты в их общепринятом обозначении. · принимать группы стоящих рядом цифр или отдельные цифры в числе за то или иное обозначение дня года · осуществлять замену одного обозначения дня на эквивалентное другое (по принципу эквивалентности). · отсчитывать порядковый номер дня в году, как от начала года, так и от конца года. При этом сумма двух дополняющих друг друга обозначений дня равна длительности года в сутках (365 или 366). · Заменять порядковый номер какого-либо дня на дополняющий номер дня – (по принципу дополнительности). · Применять при расшифровке и принцип эквивалентности и принцип дополнительности - последовательно. · Обозначать Год в шифре 2-х, 3-х или 4-х значными числами. · Совмещать начало и конец числа или слов, чтобы получать т.н. «кольцевые записи». Чтение кольцевых записей чисел, слов или составляющих их частей в обоих направлениях корреспондируется с отсчетом времени в календарных системах, состоящих из вложенных циклов различной длительности (год, месяц, неделя, день), так как движение во времени к концу цикла вместе с тем является движением к началу аналогичного цикла. При “обратном” (справа налево) чтении числа его тайный смысл, как правило, меняется на противоположный. Если по шифру сценария, например, 52 - это война, то 25 - мир; если 18 - рождение, то 81 - смерть.
Так как история представляет собой совокупность событий, происходящих во времени, а точные временные координаты событий суть числа, то параллельно с событийным сценарием, описываемым словами, а скорее и до него, небесный сценарист должен был разработать числовой сценарий мировой истории, объединив в итоге Слово (logos) и Число (arithmos). Все, что было и будет сказано, написано, открыто и создано людьми, изначально содержится в численно-событийном сценарии Мирового Разума (МР). Замена букв слова их порядковыми номерами в алфавите современного русского языка выявляет дифференциальную числовую характеристику слова. Создатель учения о логарифмах шотландский математик Джон Непер (1550 - 1617) предложил термин “логарифм”, трактуя перевод этого слова, как “отношение специфических чисел”. Обычное деление двух чисел, являющихся дифференциальными числовыми кальками слов (определение отношения специфических чисел), так же как и логарифмирование числовых калек слов, является эффективным способом познания эзотерического содержания чисел и слов.
На Руси на старославянском - «В начале было Слово, и Слово было у Бога, и Слово было Бог» (гл.1 ст. 1). В течение двух тысячелетий сокровенный эзотерический смысл Слова Божьего оставался “тайной за семью печатями”. Покажем, что за дифференциальным цифровым представлением Слова скрывается слово Число. Заменив в слове Число первые две буквы их порядковыми номерами в современном русском алфавите, получим:
2510CЛО.
Цифры 5 и 1 в комбинированной записи слова число соответствуют буквам Д и А. Цифра 2 соответствует букве Б русского алфавита, по звучанию совпадающей со второй буквой латиницы В, идентичной по написанию с третьей буквой кириллицы В. В старославянской кириллице В как цифра обозначает 2. Все эти буквы (Б, В, B) произошли от буквы β греческого алфавита, что в итоге предопределяет взаимозаменяемость букв Б и В и цифр 2 и 3 в коде. Замены Б-В и 2-3 являются наиболее употребительными. Так как цифра 0 в написании идентична букве О, то после перестановок (прием эзотерической нумерологии) с учетом исходного слова можем написать:
ДА, СЛОВО – ЧИСЛО и СЛОВО ДА ЧИСЛО (1)
Существует слово, объединяющее слово и число. Это слово – ЛОГАРИФМ (СЛОВО – logos, ЧИСЛО - arithmos). Полученные расшифровки, по сути, являются подсказкой: для того, чтобы познать тайную сущность СЛОВА, необходимо прологарифмировать числовой аналог СЛОВА. Чтобы узнать, какое же число было в НАЧАЛЕ, вновь учтем, что буква О идентична по написанию цифре 0, а слово логарифм объединяет корни двух указанных греческих слов и прологарифмируем числовое представление слова СЛОВО, предположив, что операция логарифмирования позволяет выявить связь между СЛОВОМ и ЧИСЛОМ: lg1913030 = 6,281722. Чтобы у дешифровщика не возникло сомнений, что в логарифме СЛОВА 6,28 – это первых три цифры значения 2π, за первыми тремя знаками 2π следует 17 – порядковый номер буквы p кириллицы, идентичной в письме букве π греческого алфавита, от которой она и происходит и цифра 2. В итоге 1722 (2 17 2 после перестановки) может быть прочитано, как «2π дважды». Так как цифра 6 соответствует букве е кириллицы, а цифры 2 и 3 по шифру взаимозаменяемы, то начало (6-е) и конец (3) логарифма СЛОВА означают «e трижды». Чтобы дешифровщик понял, что буква e соответствует общепринятому обозначению основания натуральных логарифмов (ОНЛ), в кольцевой записи логарифма СЛОВА после «e трижды» читаются первые 5 знаков (2,7182) значения e. Бог, у которого “было СЛОВО”, умел логарифмировать и знал значения π и е? В настоящее время обучение логарифмированию, числа π и е служат элементами школьного образования. И надо полагать, что СЛОВО намного древнее Иисуса, а Знание, заключенное в СЛОВЕ Бога (Мирового Разума), должно быть существенно сложнее школьного знания ныне живущих. На многочисленных примерах можно показать, что не только е и π, но и другие, используемые сейчас общепринятые в науке символы для обозначения математических и физических величин, изначально заданы в сценарии и используются для этих же целей. Так, таинственные Алфа(α) и Омега(ω) в Апокалипсисе Иоанна Богослова обозначают: α - мировые физические константы (постоянную тонкой структуры и константу гравитационного взаимодействия), а ω – угловые скорости вращательных движений Земли и угловую скорость вращения Вселенной [2]. С учетом вышеизложенного числовую кальку слова СЛОВО – 1913030 в буквенном виде можно представить как А3 АБ ОВО и Аз АБ ОВО. В первом варианте АЗ является аббревиатурой словосочетания Абсолютное Знание, во втором читается как старославянское Аз (личное местоимение Я). На слух последние 5 букв воспринимаются как широко известное латинское выражение ab ovo (от яйца, с самого начала ), поэтому с учётом идентичности звучания бывшее в начале всего сущего СЛОВО означает: Абсолютное Знание от начала начал; Я от начала начал. Подставив эти расшифровки в (1), получим: Да, Абсолютное Знание от начала начал – ЧИСЛО; Да, Я от начала начал – ЧИСЛО. (2) Так как согласно Иоанну Богослову ‘‘Слово было у Бога, и Слово было Бог’’, то из (2) следует, что Бог – изначальное Абсолютное Знание, выраженное в числах и словах.
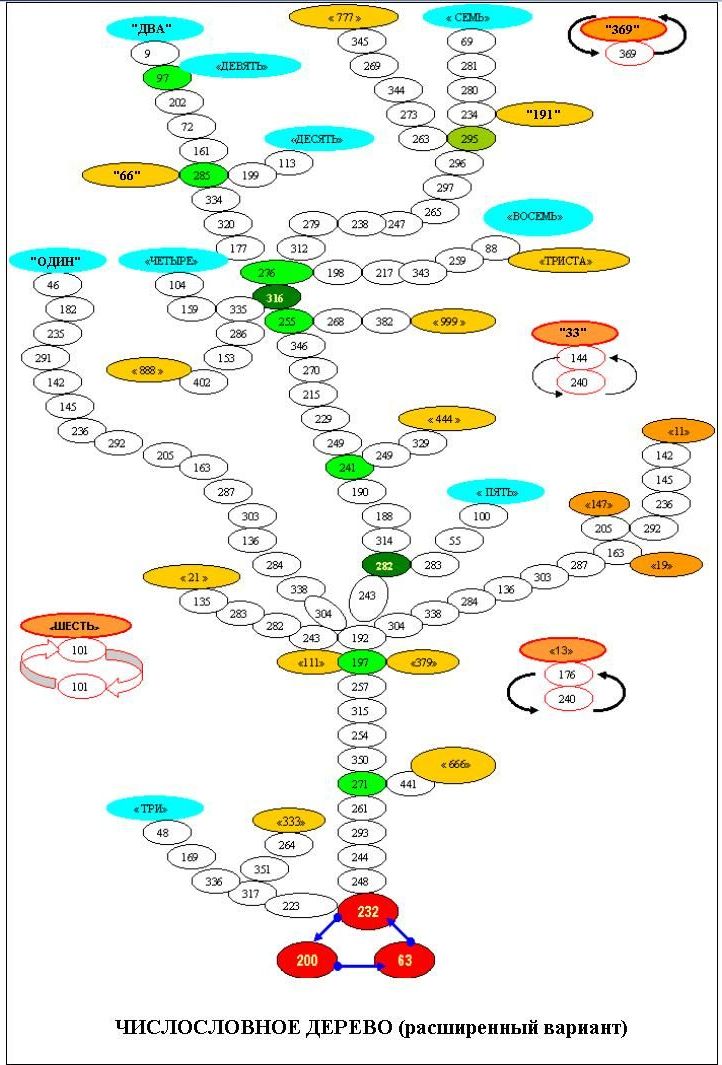
Под Абсолютным Знанием Бога необходимо подразумевать не только научное физическое знание об устройстве мироздания, строении материи и мировых константах [1], но и эзотерическое знание о будущем, предопределенным так называемыми Планами Господними. Нельзя не отметить, что В.И. Пьяновым проделана великолепная работа, значительно расширяющая наши познания как в нумерологии, так и в понимании эзотерических методов расшифровки числовых и словесных объектов. ----------------------------------///---------------------------------------- А теперь мы перейдём к теме статьи о Числословном Дереве. Переплетающися с темой В. И Пьянова вопросы расшифровки чисел «Числословного дерева» (см. рис.1) стоят здесь также остро, как расшифровка фразы «Вначале было Слово…» Почему – мы увидим дальше. А сейчас о том, что же такое – ЧИСЛОСЛОВНОЕ ДЕРЕВО (ДРЕВО)?
Числословное Древо – это результат многократных преобразований ИСХОДНОГО ЧИСЛА (или же Цифры) в своё числительное, которое затем снова превращается (по-буквенно!) в сумму чисел, соответствующих порядковым номерам каждой из букв этого числительного; Далее, вычисленное таким способом, суммарное число ВНОВЬ записывается в словесной форме (в виде числительного), а вся процедура, описанная выше, повторяется вновь и вновь, пока…. Вот именно! …. Пока что?!! Перед началом этого эксперимента у меня было ощущение, что данная процедура – бесконечна, т.е. мы никогда не дойдём до какого-либо конца. А значит, это будет бессмысленный эксперимент. Далее мне, почему то, подумалось, что, возможно, некоторые числа в результате этой процедуры (может быть) будут иметь окончание. Но, в итоге, мы получим только наборы кодовых цепочек, никак не связанных друг с другом, либо имеющих редкие пересечения… И, что это нам даст??! И, наконец, мне пришла на ум спасительная мысль о том, что для начала можно ограничиться экспериментом только лишь с одними Первоцифрами, так как все остальные числа могут быть сведены к ним простым нумерологическим сложением.
Итак, я взялся за дело, вручную выписывая и складывая цифры и буквы, числительные (и им соответствующие суммы). Работа потребовала большого количества внимания, времени и терпения. Одна ошибка по ходу перекодировок отбрасывала назад всё работу… Тем не менее в итоге получилось ЧИСЛОСЛОВНЕЕ ДРЕВО, представленное на главном рисунке (см. выше), в котором на самом верху СЛОВОМ или подчёркнутой цифрой ( в кавычках и в ОВАЛЕ) показаны анализируемые исходные Цифры и Числа, для которых и проводилась упомянутая выше процедура многократных перекодировок. В кружках, которые опускаются (от ОВАЛОВ) всё ниже и ниже – представлены (тоже в виде чисел!) результаты цифровой кодировки числительного. Эти результаты для экономии места - не писались, но, упомянутым способом, - отображалось. На самом же деле, каждое из таких чисел (в малых кружках) писалось отдельно в виде числительного, а вместо букв в нём потом ставились цифры и числа, и затем их сумма снова вписывалась в малый кружок (число – вместо числительного). И… процедура повторялась вновь и вновь…
Когда всё было сведено в один рисунок, стали появляться удивительные картинки и напрашиваться странные выводы: Практически все Первоцифры и большое число Чисел (кроме «6» и ряда Чисел !?) вписалось – таки в числословное дерево в виде индивидуальных «веточек» на общем стволе. Самым удивительным явлением оказался «корень» Числословного Дерева, представленный совершенно конкретной ТРОЙКОЙ чисел (или числительных): 232, 200 и 63, которые ВКРУГОВУЮ превращаются только друг в друга???! Такой «корень» или «ЯДРО» числословного дерева вызывает законный вопрос: «А почему именно эти числительные, числа или эквивалентные им (в числовом исчислении) слова являются центром всего этого, столь сложного строения? Случайность ли это? Что за этим стоит? Встретилось явление «ОТПАВШИХ ЛИСТЬЕВ», когда некая цифра или Число сразу (или через небольшое число этапов) «окукливаются и НЕ ВХОДЯТ(!) в структуру Числового Дерева, существуя отдельно: Это, в частности, цифра «6», числа «13», «33», «369»… Кстати, не в этом ли суть неприязни людей к некоторым конкретным числам. Не исключено, что некоторые люди просто чувствуют это! Естественно, что одному и тому же числительному (числу) могут соответствовать в русском языке разные СЛОВА, связь и общность которых ещё надо проверять… Например, сразу выявилось, что числу «97» соответствуют эквиваленты {9}, {302}; А числу «285» - эквивалентные числительные {66}, {811} и {990}; Числу «192» соответствуют эквивалентные числительные {52}, {403}, {68}, {304}… Проще говоря, на числовом дереве обнаружились «ТОЧКИ ВЕТВЛЕНИЯ», представляющие несомненный семантический интерес
В отношении Числословного Дерева можно выдвинуть некоторую гипотезу, которая состоит в том, что, по крайней мере, достаточное количество чисел в своём словесном обличии (в виде числительных) могут быть эквивалентны как между собой, так и просто соответствующему ЧИСЛУ. Можно также предположить, что несовпадения имеют место только для тех числительных, где сумма порядковых номеров букв, из которых состоит данное числительное, не равна формальному числу «Х», так как был нарушен некий гипотетический исходный порядок букв в алфавите. В этом случае, специальным исследованием, было бы интересно установить тот истинный порядок и конкретные буквы алфавита, которые, возможно, были задействованы в Числословном Дереве изначально и, которые могли бы снять несоответствия - чисел и их числительных Тем не менее, по крайней мере, для некоторых узловых точек Дерева такая эквивалентность, почему-то, ещё соблюдается. Рассмотрим для примера число «Х =285» ~ Двести восемьдесят пять = {285}; Здесь и далее будем иметь ввиду, что фигурные скобки { } - это условная, цифровая, запись числа 285 в виде числительного. В чём состояла идея эксперимента? ИСХОДНОЕ число - 285 мы попытаемся представить в виде сумм нескольких (фиксированных) слагаемых чисел, для которых нам известны их числительные имена. Далее, подразумевая мысль, что тем самым, косвенно, проверяется Алфавит, мы произведём переход в формально-числовую форму, где сложению (вычитанию) нами подвергаются уже словесные формы: {Х} + {Y}. Результат будет являть собой некое «синтетическое» числительное: {X} +{Y} = {{X+Y}} = {{Z}}.. которое во всех формах своего представления (ПО ИДЕЕ!) должно быть равно исходному числу «285». В итоге получилось несколько комбинаций, как подтверждающих идею эксперимента, так и отрицающих её: (285) = {66} --- {60}+{6} --- (184 + 101) = 285! {811} --- {800} + {11} --- (143 + 142) =285! {811} --- {810} + {1} --- ( 256 + 46) = 302?!! {811} --- {801} + {10} --- ( 189+113) = 302?!! {990} --- (900} + {90} --- 152 + 133 = 285! {199} --- {100} + {99} --- 55 + 230 = 285! {199} --- {100} + {90} + {9} --- 55 + 133 + 97 = 285! {199} --- {190} + {9} --- 188 + 97 = 285! {199} --- {109} + {10} --- 152 + 133 = 285!
{337} --- {300} +{30} + {7} --- (88+128+69) = 285! {337} --- {330} + {7} --- (216+69) = 285! {337} --- {300} + {37} --- (88+197) = 285! {337} --- {307} +{30} --- (157+128) = 285!
Таким образом, было найдено, например, что эквивалентность числа и слова могут давать, в частности, такие соответствия числительных: 285 = {66} = {811} = {990} = {199} = {337}… Однако, не все (выбранные мною) числительные дают аналогичный результат. Действительно, число 285, например, можно представить себе по–разному: Посмотрите варианты - А, В, С и D: А). 285 = (69 +48) + (9 +159), откуда следует сложение числительных: ({7} + {3}) + ({2} +{104}) = {10} + (106} = (113 + 156) = 269; Или же: В). 285 = (163 – 46) + (113 + 55), откуда следует сложение числительных: ({204} - {1}) + ({10} + {100}) = (167 + 168) = 335; Или же: C). 285 = (69 + 48) + ( 104 + 64); откуда следует сложение числительных : ({7} +{3}) + ({4} + {102}) = (113 + 156) = 269; Или же: D). 285 = (69 + 48) + (113 +55); откуда вытекает сложение числительных : ({7} +{3}) + ({10} + {100}) = {7} + {3} = {110} --- (69 + 18 +168) = 285!
Можно сделать вывод, что от комбинаций слагаемых {Xi} результаты очень даже зависят, хотя можно получить и правильные результаты, т.е. точность здесь весьма неоднозначна, ХОТЯ ОНА И ВСТРЕЧАЕТСЯ! НО, ПОЧЕМУ ЭТО ТАК?!!
Сказанное выше даёт мне основания предполагать, в частности, что: Древний русский алфавит, который , как мы точно знаем, был раньше – другим, возможно был другим прежде всего в том, что он был точно и однозначно СЧИСЛИМЫМ математически. Если на таком алфавите говорилось «Двести тридцать два», то числовая калька этого слова счислялась как «232»! СЧИСЛИМЫЙ математически алфавит - на сегодняшний день, в принципе, МОЖЕТ БЫТЬ синтезирован и ИСКУССТВЕННО, если применить к этому мою методику Числословного Древа, программирование и компьютерную технику!
А пока приходится, констатировать, что результаты моих экспериментов непонятным образом зависят и от перестановок, демонстрируя таким образом, что математика СЛОВ и математика Цифр, к сожалению, не всегда совпадают… Это иллюстрирует, например, ещё один мой расчётный эксперимент, который представлен ниже:
Рассмотрим сложение, например, такой последовательности: {7} + {3} + {10} + {100} = ???, (Здесь в фигурных скобках даны (в форме цифр!) даны «слова–числительные», для которых мы будем искать полные суммы цифр, соответствующих буквам этих числительных…)
{7+3}+ {10} +{100} --- (69 +48) + (113) + (55) = 281; {7 +10} + {3} +{100} --- 135 +48 + + 55 = 238; {7+100} + {3 + 10} --- 124 +144 = 268; {7 + 100} +{3} + {10} --- 124 + 48 + 113 = 285; {7+10+100} + {3} --- 190 + 48 = 238; {3+10+100} + {7} --- 199+69 = 268; {3+100} + {7+10} --- 103 + 135 = 238;
Получились, увы, весьма неоднозначные результаты… ОСТАЁТСЯ ТОЛЬКО РАЗМЫШЛЯТЬ И ИСКАТЬ причины того, что именно есть общего между теми комбинациями, которые дают идентичные (правильные) результаты и что именно порождает в них отличия (неправильность результата)…. К сожалению, эти исследование пока не закончены… Выводы: Числословное Дерево, тем не менее, уже сейчас можно использовать для исследования не только вопросов синхронизированности (идентичности) сложения собственно чисел и их числительных (на предмет выявления роли алфавита в проблеме СЧИСЛЕНИЯ ИСТИНЫ), но и анализировать сами числа… Например, возможно построить числословные деревья для особых чисел, например, для чисел из строк магических квадратов, включая прямое (привычное) прочтение цифр этих чисел, а также зеркальные написания тех же цифр исследуемых чисел. Можно использовать числословные деревья и для изучения семантических проблем, переходя с их помощью в плоскость анализа эквивалентных числовых форм представления изучаемых словесных форм. Числословные деревья могут также служить инструментом исследования экспериментально полученных чисел, когда конечной целью будет нахождение эквивалентных (числам) – словесных форм, а также для окончательного анализа нужных СЛОВЕСНЫХ форм представления, например, с рекламных позиций.
К слову сказать, на основании уже имеющегося у меня словаря (~25000 слов) представляет немалый интерес прочтение словесных эквивалентов чисел, лежащих в основе, (в «корне», в «ядре») Числословного Древа (и / или чисел непосредственно примыкающих к этой ЗАГАДОЧНОЙ Тройке Чисел - 63, 200, 232).
Вот некоторые из них (пока без моих комментариев). Но, при этом, каждый может попробовать найти свою (а может быть и НАШУ?!!) Истину.
Корнеев А. А. Москва, 1992 г.
Все статьи Алексея Корнеева: Алгоритм вычисления Хлебниковских струн Времени Египетские пирамиды с позиций числонавтики Голографическая интерпретация наноструктурного феномена Дона Айглера Струны Времени Велимира Хлебникова и их исследование О ЦИФРАХ И ЧИСЛАХ ЗАМОЛВЛЮ Я СЛОВО ЧИСЛОСЛОВНОЕ ДЕРЕВО (Расширенный вариант) Числонавтика. Цифровые явления и понятия (ч.1)
|